Normalizing Flows and Its Friends (Part 2)¶

What is normalizing flows?¶

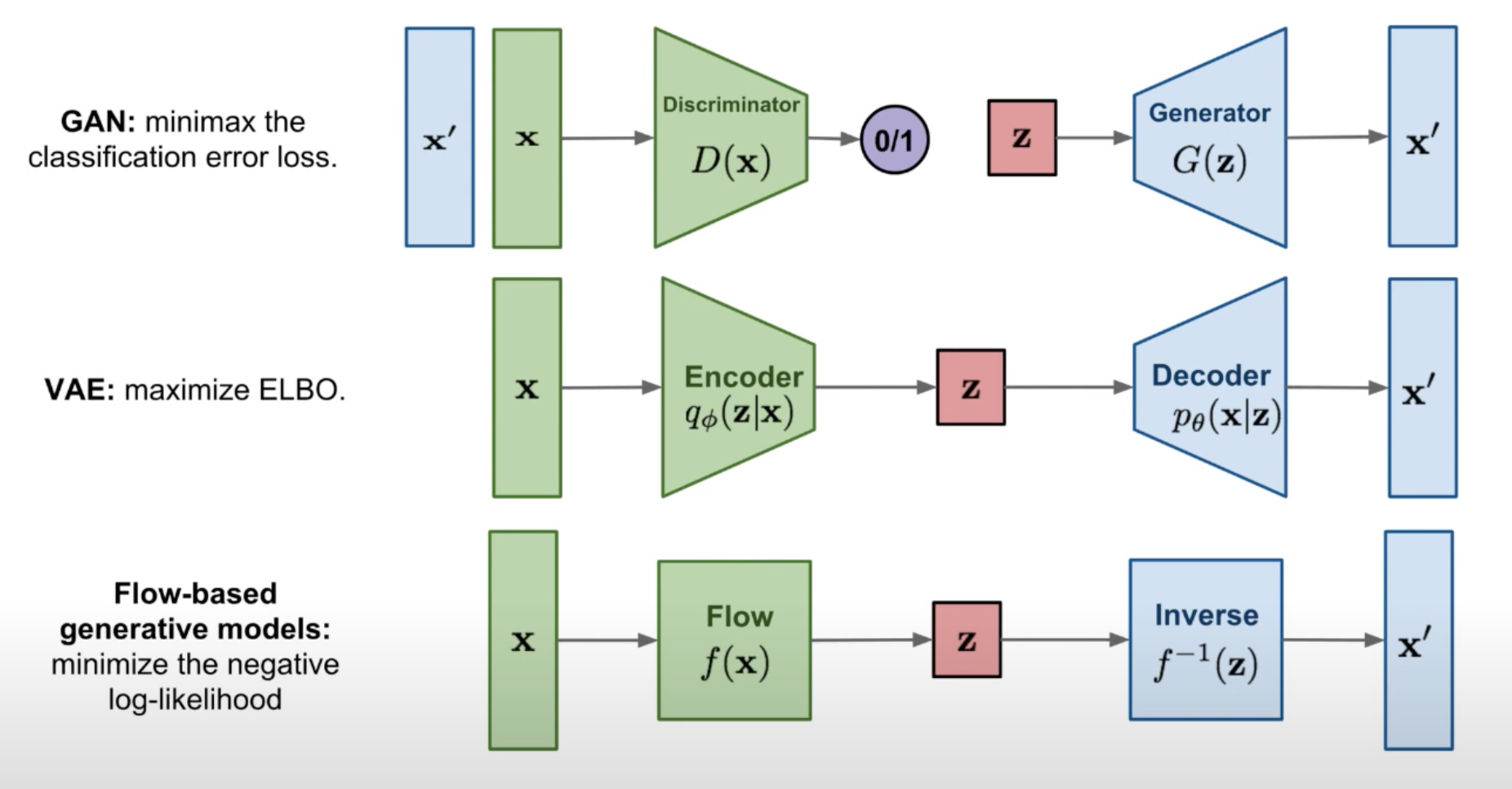
Triplet

One type of generative models is flow-based models, which explicitly learns the mapping between a group of samples $x_{1}$ , $x_{2}$ , ..., $x_{n}$ to their latent distribution $p(x)$ .

Normalizing flows is one example of flow-based models.

Why normalizing flows?¶

Given some real world data samples, we are always interested in learning its underlying distributions. Knowing the exact data distribution $p(x)$ is helpful in some scenarios such as sampling data and identifying bias.

Objective

To minimize some notion of distance between $p_{D}$ and $p_{M}$

Given a dataset $X=x_{1}, x_{2}, x_{3}, ...$ from an underlying distribution $p_{D}$ ,
Can we find an approximating distribution $p_{M}$ , which is from a family of $M$ and parametrized by $\theta$ , to minimize the distance between $p_{D}$ and $p_{M}$ ?
Mathmatically, it is written as below
$\theta^{*}=\underset{\theta \in M}{\mathrm{argmin}} \space dist(p_{\theta}, p_{D}$)$
If KL-divergence is the distance function, the above equation becomes the maximum likelihood estimation ...
$\theta^{*}=\underset{\theta \in M}{\mathrm{argmin}} \space E_{x~p_{D}} [-log \space p_{\theta}(x)]$

Flow-based models are different than GAN or VAE, since Flow-based models explicitly learn $p(x)$ by optimizing the log likelihood.

In GAN, the probability density function estimation is implicit by having the minmax classification error. We don't explicitly assign a probability density function and estimate it.

In VAE, we get an approximate probability density function by optimizing the evidence lower bound (which is $p_{\theta}(x|z)$ ). The encoder captures the approximate posterior mapping between $x$ and $z$ , which is $q$ parameterized by $\phi$ . The decoder captures $p_{\theta}(x|z)$ which is parameterized by $\theta$ . In this casce, it is an approximate density estimation.

In short, both GAN and VAE do not explicitly learn probability density function of real data $p(x)$ .

In flow-based models, given an $x$ , we want to find the function $f$ to get the latent representation $z$ . And if we invert $f$ , we will get $x$ back. The function $f(x)$ and $f^{-1}_(x)$ are exactly the inverse. And the flow-based models try to capture $f$

How does it work?¶

z to x

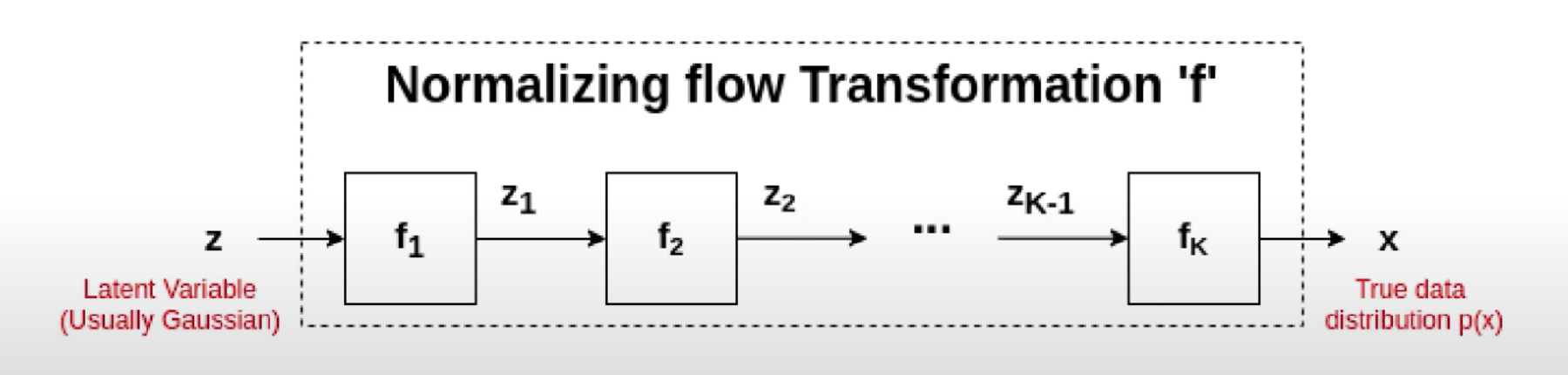
We try to identify a transformation $f: Z \rightarrow X$ where f is a series of differentiable and invertible functions ( $f_{1}$ , $f_{2}$ , ..., $f_{K}$ ,)

In general, for any invertible function $f: Z \rightarrow X$ , the probability function is below. The detailed steps can be found in this page

$p(x') = \pi(z') \mid {det(J_{f^{-1}})} \mid$

$log \space p(x') = log \space \pi(z') + \sum^{K}_{i=1} log \mid {det(J_{f^{-1}})} \mid$

Intuition:

The first term describes the transformation $f$ moulds the density $p_{Z}(z)$ into $p_{X}(x)$ .
The second term describes the relative change of volume around $z$

In summary, the three requirements must hold for a normalizing flow model:

Transformation function $f$ should be differentiable
Transformation function $f$ should be invertible
Determinant of Jacobian should be easy to compute

Example 1: NICE (Non-linear Independent Components Estimation)¶

NICE

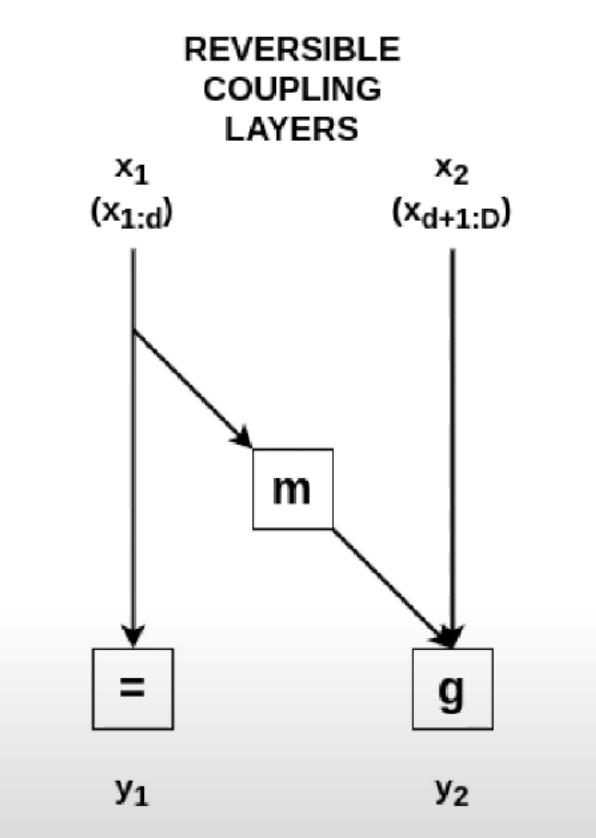
Coupling layer operation: $y_{1} = x_{1}$

$y_{2} = g(x_{2};m(x_{1}))$

Therefore, its Jacobian is a lower-triangular matrix and the determinant is the product of diagonal elements

$\frac{\partial y}{\partial x} = \begin{bmatrix} I & 0 \\ \frac{\partial y_{2}}{\partial x_{1}} & \frac{\partial y_{2}}{\partial x_{2}} \end{bmatrix}$

The inverse mappings are:

$x_{1} = y_{1}$

$x_{2} = g^{-1}(y_{2}, m(y_{1}))$

Example 2: Real NVP (Real-valued Non Volume Preserving)¶

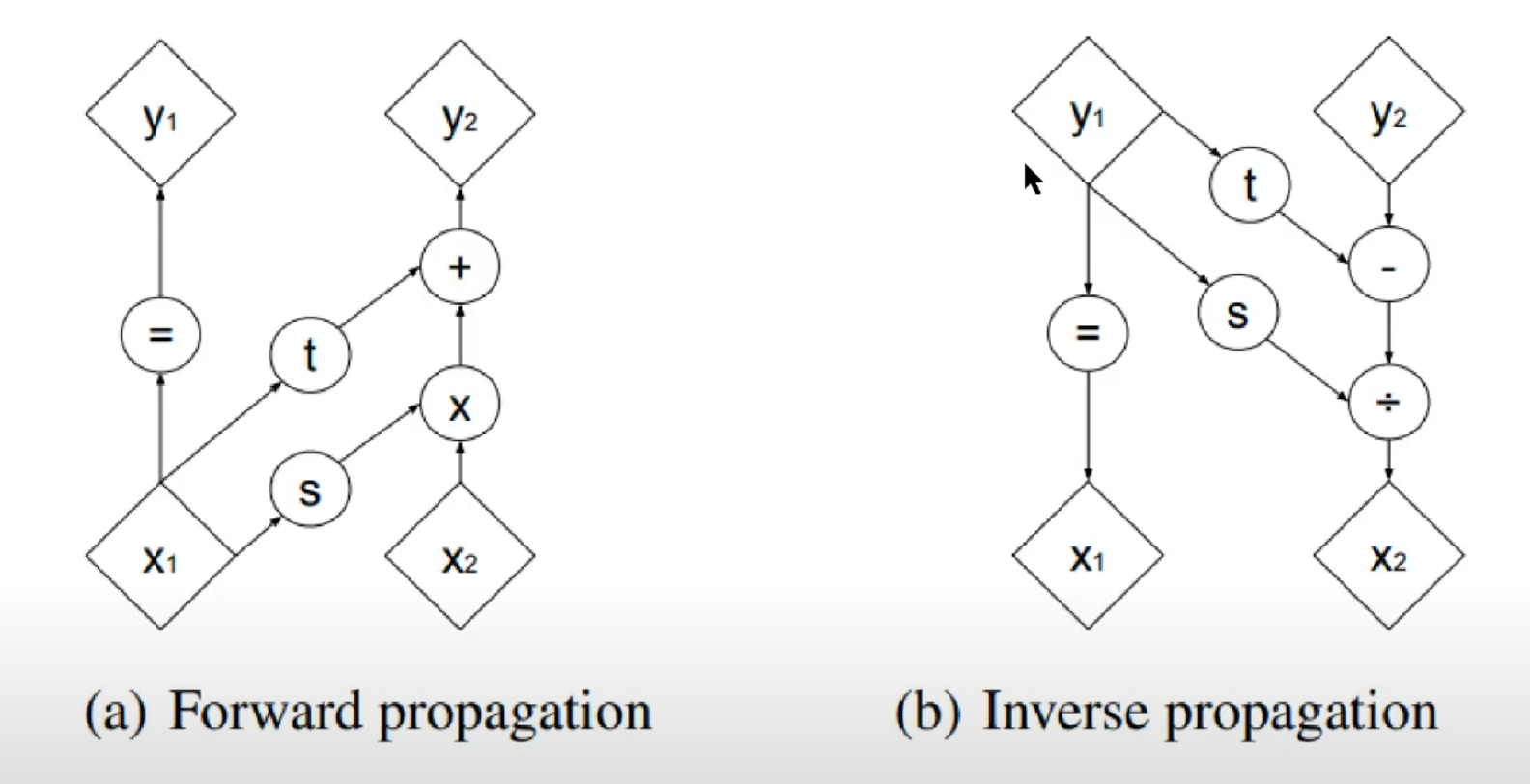
RealNVP

Affine coupling operations are (there is one translation component and one scale component for $y_{2}$ ):

$y_{1} = x_{1}$

$y_{2} = x_{2} \odot exp(s(x_{1})) + t(x_{1})$

The Jacobian becomes

$\frac{\partial y}{\partial x} = \begin{bmatrix} I_{d} & 0 \\ \frac{\partial y_{2}}{\partial x_{1}} & diag(exp[s(x_{1})]) \end{bmatrix}$

Since the Jacobian matrix is not always equal to 1, affine coupling is not always volume preserving which is more realistic in real world data.

The inverse operations are: