Normalizing Flows and Its Friends (Part 1)¶
Here is some pre-requisite knowledge required before we move to Normalizing Flows.
1. Jacobian Matrix¶
Jacobian is a just matrix containing all partial derivatives between each input and output. It looks scary, but in fact, it is just a fancy name for a partial derivative matrix.
For example, if
z = \begin{bmatrix} z_{1} \\ z_{2} \end{bmatrix}
x = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}
and
z = f(x)
x = f^{-1}(z)
then,
J_{f} = \begin{bmatrix} \frac{\partial x_{1}}{\partial z_{1}} & \frac{\partial x_{1}}{\partial z_{2}} \\
\frac{\partial x_{2}}{\partial z_{1}} & \frac{\partial x_{2}}{\partial z_{2}} \end{bmatrix}
J_{f^{-1}} = \begin{bmatrix} \frac{\partial z_{1}}{\partial x_{1}} & \frac{\partial z_{1}}{\partial x_{2}} \\
\frac{\partial z_{2}}{\partial x_{1}} & \frac{\partial z_{2}}{\partial x_{2}} \end{bmatrix}
J_{f} J_{f^{-1}} = I
2. Determinant¶
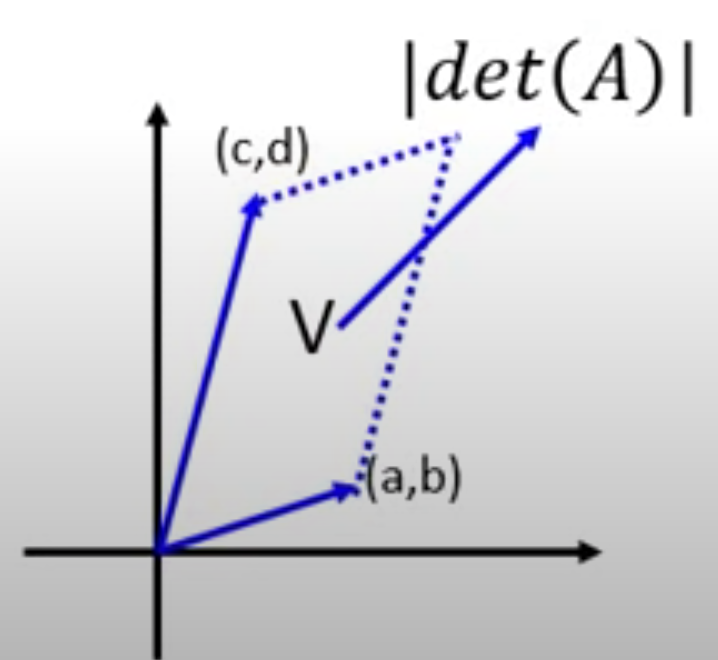
Determinant is a scalar value, which describes the area/volume enclosed by all the vectors in a matrix.
For example, if
A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}
then,
det(A) = ad - bc
The most important thing is that:
det(A) = {\frac{1}{A^{-1}}}
det(J_{f}) = {\frac{1}{J_{f^{-1}}}}
In a 2D space, it looks like this:
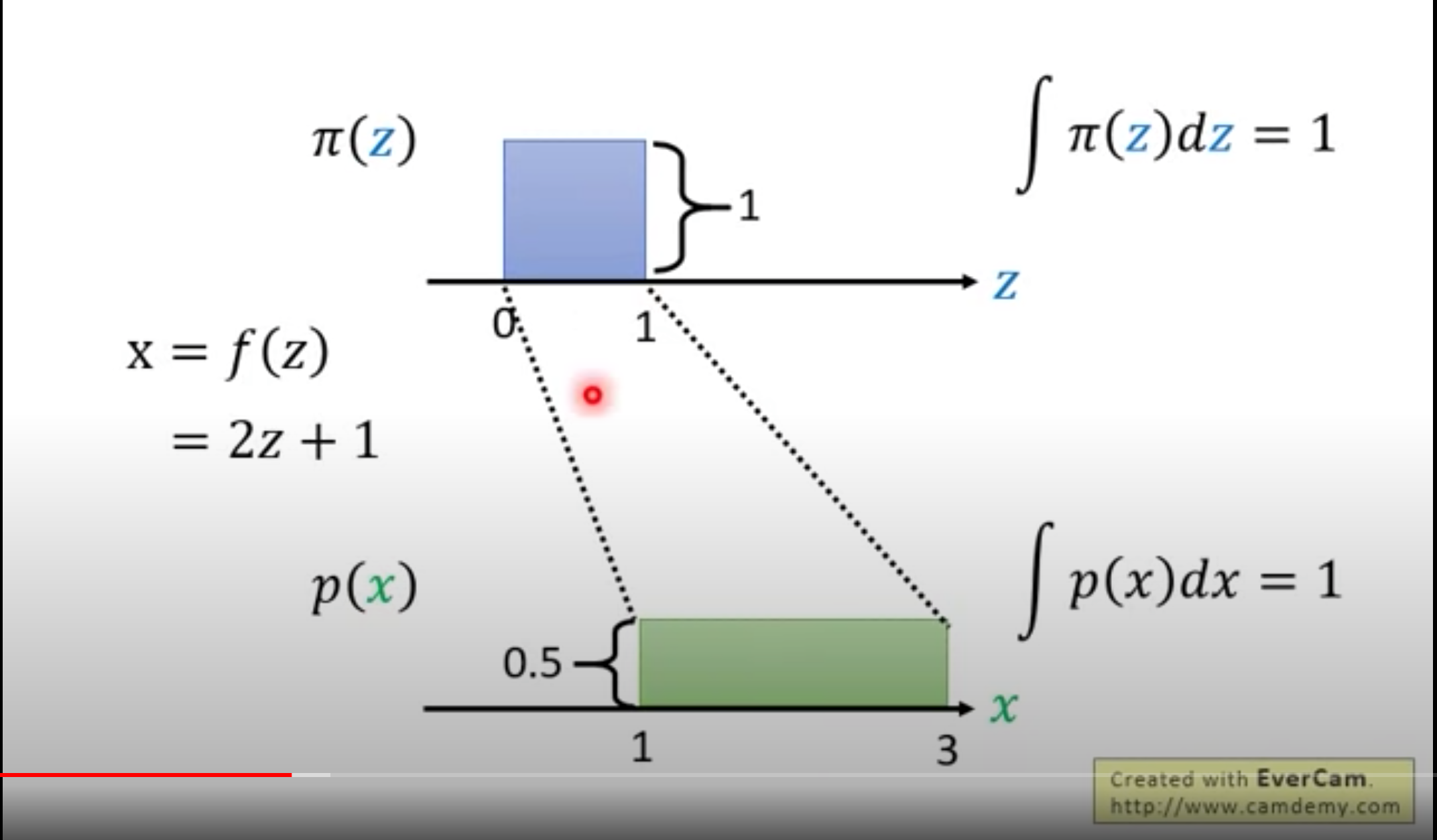
3. Change of Variable Theorem¶
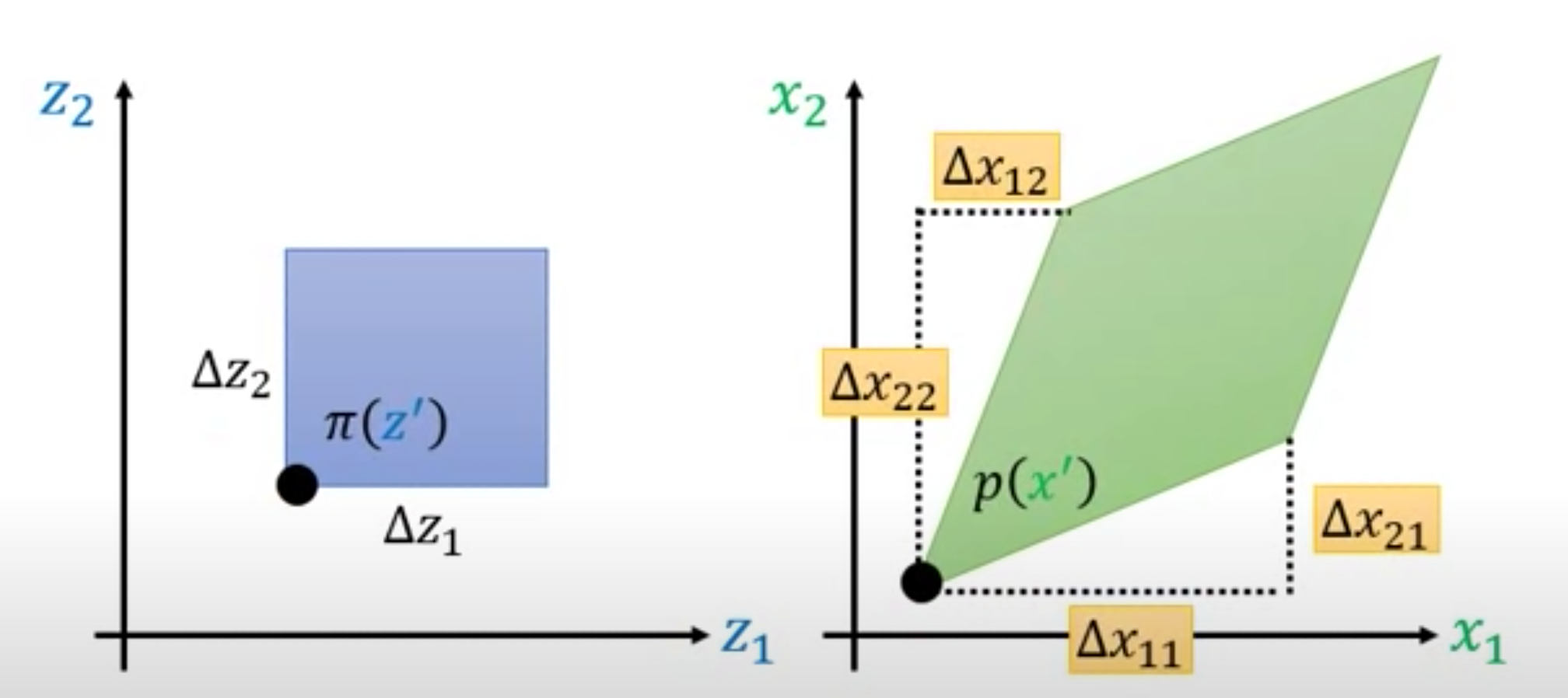
p(x') \mid det {\begin{bmatrix} \Delta x_{11} & \Delta x_{21} \\
\Delta x_{12} & \Delta x_{22} \end{bmatrix}} \mid = \pi(z') \Delta {z_{1}} \Delta {z_{2}}
and this becomes to
p(x') \mid det(J_{f}) \mid = \pi(z')
p(x') = \pi(z') \mid {det(J_{f^{-1}})} \mid